Вернуться на методику финансовая математика
Расчет оптимальной партии заказа или "Модель экономически обоснованного заказа"
(EOQ - model Economic Order Quantity)
Существуют две крайности при решении проблемы оптимальной партии заказа: делать очень редко заказ с большим количеством сырья, или частые заказы с малым количеством сырья. В первом случае минимальны затраты на оформление, доставку и т.д. партии заказа, но максимальны при хранении сырья. Во втором случае все наоборот.
Затраты на выполнение одной партии заказа можно рассчитать как:
Зат1парт = (ПотрСырья1период / Разм1парт) * СтоимРазм1зак, где
ПотрСырья1период - потребность в сырье в течение 1 периода,
Разм1парт - средний размер 1 партии заказа,
СтоимРазм1зак - средняя стоимость размещения одного заказа.
Потребность в сырье и стоимость размещения заказа величины постоянные, а размер одной партии можно менять. При увеличении размера партии затраты на приобретение сырья снижаются. В то же время чем реже закупается сырье, тем дольше оно хранится на складе и пропорционально увеличивается стоимость хранения его на складе.
Стоимость хранения сырья на складе можно определить как:
ЗатХран = (Разм1парт / 2) * ЗатХран1ед, где
ЗатХран1ед - затраты по хранению одной единицы сырья за период.
Так как стоимость хранения одной единицы сырья величина постоянная, то уменьшить стоимость хранения сырья можно только за счет уменьшения размера одной партии заказа.
Требование оптимизации по затратам на выполнение одной партии заказа и стоимости хранения сырья на складе противоположны.
Зат1парт + ЗатХран -> min
Дифференцируем по Разм1парт, для определения экстремума функции.
- 1 / Разм1парт2 * ПотрСырья1период * СтоимРазм1зак + 1 / 2 * ЗатХран1ед = 0
2 * ПотрСырья1период * СтоимРазм1зак / ЗатХран1ед = Разм1парт2
Разм1партопт = EOQ =
Из этого выражения следует, что средний размер производственного запаса будет
ПроизЗап = EOQ / 2.
Часто формулу EOQ записывают в виде:
EOQ =
EOQ - объем партии в единицах;
F - стоимость выполнения одной партии заказа;
D - общая потребность в сырье на период, ед.;
H - затраты по хранению единицы сырья.
Пример. Рассчитайте оптимальную партию заказа, при условии, что потребность в сырье составляет 450 ед. в месяц, стоимость одной поставки 1000 рублей и затраты на хранения 1 ед. в месяц равны 28 рублям.
EOQ = 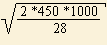 = 179 ед. = 179 ед.
Если производить закупки по 179 ед., то общие затраты на приобретение и хранения сырья будут минимальны.
Аналогично производится оптимизация для размера запасов готовой продукции. Задача минимизации текущих затрат по их обслуживанию заключается в определении оптимального размера партии производимой продукции. При производстве товара мелкими партиями затраты по хранению его запасов в виде готовой продукции будут минимальными. В то же время текущие затраты предприятия, связанные с частой переналадкой оборудования и подготовкой производства будут большими. Оптимизация совокупного размера текущих затрат по обслуживанию запасов готовой продукции может быть осуществлена на основе вышеприведенной формулы. В этом случае вместо общей потребности в сырье на период (D) используется планируемый объем производства или продажи готовой продукции, вместо оптимальной партии заказа (EOQ) будет оптимальный размер производимой продукции.
При оптимальном выборе размеров объема закупки товаров и запасов готовой продукции экономятся финансовые средства, а значит необходимо меньше оборотных средств и, следовательно, выше значение коэффициента рентабельность продаж.
Рис. 1. График оптимальной партии заказа (EOQ - model); затраты по хранению одной единицы сырья составляют 1 рубль, общая потребность в сырье: 20, 100, 1000 и 5000 единиц
На тему этой методики существуют примеры задач на расчет оптимальной партии заказа с решениями.
Программная реализация данной методики финансовой математики сделана в: "Альтаир Финансовый калькулятор 2.xx".
На примере расчета оптимальной партии заказа можно увидеть, как применять программу "Альтаир Финансовый калькулятор 2.xx" на практике.

Главная  Методики финансового и инвестиционного анализа Методики финансового и инвестиционного анализа  Финансовая математика Финансовая математика  Расчет оптимальной партии заказа Расчет оптимальной партии заказа 
Copyright © 2021 by Altair Software Company. Потенциальным спонсорам программ и проекта.
|



