Инструменты финансового и инвестиционного анализа

Задача на расчет статистических параметров

Задача №1 Для анализа финансовой отчетности исследуемого предприятия необходимо рассчитать средние значение рентабельности собственного капитала из нескольких предприятий той же отрасли промышленности и оценить степень соответствия рассчитанных значений закону нормального случайного распределения. Рентабельность собственного капитала для 12 предприятий: 23,82%; 34,19%; 27,06%; 30,44%; 26,51%; 28,19%; 24,82%; 31,76%; 26,12%; 28,31%; 30,12%; 26,34%.

Вычислим среднеарифметическое значение для рентабельности собственного капитала:
а = (а1 + а2 + ... + а12) / 12 = (23,82% + 34,19% + 27,06% + 30,44% + 26,51% + 28,19% +
+ 24,82% + 31,76 + 26,12% + 28,31% + 30,12% + 26,34%) / 12 = 28,14%;

Рассчитаем дисперсию нормального закона распределения ошибок для значений рентабельности собственного капитала:
D = ((a1 - a)2 + (a2 - a)2 + ... + (a12 - a)2) / (n-1) = ((23,82 - 28,14)2 + (34,19 - 28,14)2 + ...
... + (26,34 - 28,14)2) / (12-1) = 8.31477

Среднеквадратическое отклонение значений рентабельность собственного капитала:
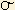Среднеквадратическое отклонение = sgrt(D) = sgrt(8.31477) = 2.88353

Коэффициент вариации для значений рентабельность собственного капитала:
V = (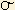Среднеквадратическое отклонение / a) * 100% = (2.88353 / 28,14) * 100% = 10.25%

Отношение показателя асимметрии к его ошибке для рентабельности собственного капитала:
A = ((a1 - a)3 + (a2 - a)3 + ... + (a12 - a)3) / (n * 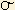Среднеквадратическое отклонение3) = ((23,82 - 28,14)3 + (34,19 - 28,14)3 + ...
... + (26,34 - 28,14)3) / (12*2.883533) = 0,528088

ma = sqrt(6 *(n-1) / ((n+1) * (n+3))) = sqrt(6 * (12 - 1) / ((12 + 1) * (12 + 3))) = 0.5817745

A / ma = 0,528088 / 0.5817745 = 0,90772

Отношение показателя эксцесса к его ошибке для рентабельности собственного капитала:
E = ((a1 - a)4 + (a2 - a)4 + ... + (a12 - a)4) / (n * 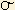Среднеквадратическое отклонение4) -3 = ((23,82 - 28,14)4 + (34,19 - 28,14)4 + ...
... + (26,34 - 28,14)4) / (12*2.883534) - 3 = - 0,516749
me = sqrt(24 * n *(n-2) * (n-3) / ((n-1)2 * (n+3) * (n+5))) = sqrt(24 * 12 * 10 * 9 / (112 * 15 * 17)) =
= 0,916547

E / me = -0,516749 / 0,916547 = - 0,5638

Среднее линейное отклонение значений рентабельности собственного капитала:

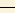
a = (|a1 - a| + |a2 - a| + ... + |a12 - a|)/n = (|23,82 - 28,14| + |34,19 - 28,14| + ...
... + |26,34 - 28,14|) / 12 = 2.36167

Ответ. Среднеарифметическое значение рентабельности собственного капитала будет равно 28,14%. Коэффициент вариации равный 10.25% и среднее линейное отклонение значений равное 2.36167 соответствуют небольшому разбросу исследуемых значений. Так как значение отношение показателя эксцесса к его ошибке и отношение показателя асимметрии к его ошибке меньше 3 то анализируемая информация подчиняется закону нормального распределения.

Для задач на эту тему есть методика финансового анализа для расчета дисперсии, среднего арифметического, среднеквадратического отклонения, коэффициента вариации, используемая при решении задач финансовой математики.


Главная Задачи по экономике Расчет статистических параметров
Copyright  © 2021 by Altair Software Company. Потенциальным спонсорам программ и проекта.
 
Финансовый анализ: финансовая математика, анализ хозяйственной деятельности предприятия, факторный анализ, инвестиционный проект.Методики финансового анализа: облигации, вексель, аннуитет, сложный процент, рентабельность, ликвидность, инвестиции, платежеспособность, леверидж.Программы финансового анализа серии Альтаир: Финансовый калькулятор, Анализ финансовой отчетности, Оптимизация структуры капитала.Задачи по экономике, по финансам, по инвестициям.Электронная экономическая библиотека, экономическая теория, книги по экономике, литература.Статьи о финансовом анализе, Статьи по экономике.Финансовый калькулятор On-line.FAQ о сайте Инструменты финансового анализа и программах Альтаир.

Добавить сайт "Инструменты финансового и инвестиционного анализа" в Избранное/Закладки